Introducción

Esto es una guía para aquellos que parten en el mundo de la programación competitiva.

Se planea cubrir los paradigmas básicos que se enseñan en los cursos de Taller de Programación Avanzada/Competitiva IIC255 y IIC2553 de la Pontifica Universidad Católica de Chile.

Espero les sea de utilidad y se maravillen.

— Warp.

C++ en Programación Competitiva

C++ es el lenguaje más usado en la programación competitiva. Esto se debe a su rapidez en tiempo de ejecución, que es junto con el límite de memoria, una de las restrcciones que se solicitan en los problemas de programación.

Instalación

C++ es un lenguaje compilado, es decir, un lenguaje que requiere de primero de ser pasado a un archivo de código máquina o ejecutable.

Windows

Pueden instalar g++ utilizando MYSYS2 con la siguiente guía.

Linux/Mac

Normalmente los sistemas unix ya traen consigo el compilador g++. Para revisar si lo tienes instalado puedes ocupar

g++ --version

y si ya lo tienes instalado te aparecerá algo como

g++ (GCC) 12.1.0

En caso que no te aparezca esto, puedes colacar instalarlo colocando en tu terminal;

brew install gcc

Ubuntu/Debian

sudo apt install g++

ArchLinux

sudo pacman -S g++

Uso

Creamos el archivo hola_mundo.cpp

#include <iostream>
using namespace std;

int main() {
  cout << "¡Hola mundo!" << endl;
  return 0;
}

luego abriendo la terminal en el directorio donde se guardó este archivo, tienes que correr el comando

g++ hola_mundo.cpp -o hola_mundo.out

esto creará un archivo ejecutable llamado hola_mundo.out. Entonces podemos utilizar

./hola_mundo.out

para ejecutar el programa ya comilado.

¡Hola mundo!

Template de C++

La template que yo ocupo es:

#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
using namespace std;
#define rep(i, n) for (int i = 0; i < n; ++i)
#define rep_(i, k, n) for (int i = k; i < n; ++i)
using ll = long long;

int main() {
  ios_base::sync_with_stdio(false);
  cin.tie(nullptr);
  cout.setf(ios::fixed);
  cout.precision(10);
  
  // Solución aquí
  
  return 0;
}

Explicación

#pragma GCC optimize("Ofast"): hace optimizaciones internas al momento de compilar.
#include <bits/stdc++.h>: nos importa la basta mayoría de herramientas (estructuras de datos y funciones varias) que se ocupan en programación competitiva.
using namespace std: indicamos que vamos a utilizar la librería estándar.
#define rep...: nos crea alias para las funciones que queramos. En este caso hacemos alias para los for.
using ll = long long: alias para el tipo de dato long long.
ios_base::sync_with_stdio(false)...: optimizamos el uso de cin y cout. Esto hace que se imprima en pantalla cuando ya se hallan entregado todo los inputs al programa. Se debe quitar en problemas interactivos.
cout.precision(10): indicamos que los números después de la coma a imprimir son 10.

Recursión

La recursión es una técnica de programación que se utiliza para resolver problemas de forma muy elegante. La idea es pensar en una función que se llama a sí misma hasta que se alcanza la solución.

La recursón debe poseer un caso base, el cual va a ser la última vez que se llame a la función. Caso contrario, nuestra función no terminaría.

De buenas a primeras no es tan fácil ver la recursión en los problemas, por lo cual es útil revisar unos típicos algoritmos de ejemplo.

imagen

Secuencia de fibonacci

Es una secuencia muy conocida en el mundo matematico, la cual se define de forma recursiva como:

\( f_0 = 0 \)
\( f_1 = 1 \)
\( f_n = f_{n-1} + f_{n-2} \quad \forall n \geq 2 \)

Podemos echar un poco las cuentas y ver que la secuencia va de la siguiente forma: \( 0, 1, 1, 2, 3, 5, 8, 13, 21, \ldots \)

En código

Podemos ocupar la siguiente función definida en python para calcular la secuencia de fibonacci:

def fibonacci(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci(n-1) + fibonacci(n-2)

print(fibonacci(10))

Como es claro, los casos base son los dos primeros valores de la secuencia. Mientras que el resto se calcula revisando el valores de los anteriores valores de la secuencia.

En C++ el código sería el siguiente:

#include <iostream>
using namespace std;

int fibonacci(int n) {
  if (n == 0) {
      return 0;
  } else if (n == 1) {
      return 1;
  } else {
      return fibonacci(n-1) + fibonacci(n-2);
  }
}

int main() {
  cout << fibonacci(10) << endl;
  return 0;
}

Desventaja

El problema con esta implementación es que se están calculando mismo valores de la suceción varias veces.

Podemos hacer un dibujito de las llamdas que hace nuestra función fibonacci.

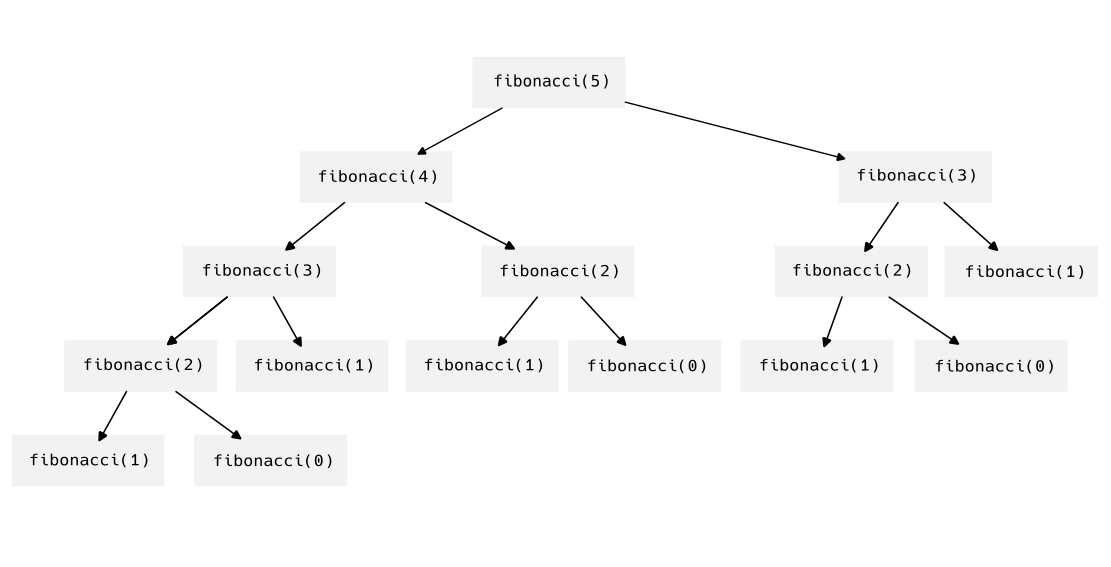
fibonacci llamadas

Se aprecia que, por ejemplo, se calcula fibonacci(3) dos veces que no está mal. Pero notemos que fibonacci(2) se llega a calcular tres veces. Para números más grandes este problema se vuelve peor. De hecho la complejidad de esta función es de \( \mathcal{O}(\phi^n) \), donde \( \phi = \frac{1+\sqrt{5}}{2} \). Ya que la cantidad de llamadas para fibonacci(n) es precisamente el número de fibonacci \( n \), que por una fórmula conocida es \[ f_n = \frac{ (\phi)^n - (\Phi)^n }{\sqrt{5}} \] donde \( \Phi = \frac{1-\sqrt{5}}{2} \).

Más adelante veremos una solución a esta situación. Pera adelantamos desde ya que dicha optimización hace que el algoritmo se vuelva de complejidad lineal.

Generar subconjuntos

Veamos cómo generar todos los subconjuntos de un conjunto dado.

Supongamos por simplicidad que tenemos un conjunto de elementos \( \{1, 2, 3\} \), luego sus subconjuntos son \( \emptyset, \{1\}, \{2\}, \{3\}, \{1, 2\}, \{1, 3\}, \{2, 3\}, \{1, 2, 3\} \).

Para ver la recursión hay que pensar en un argumento que nos proporcione una información útil. En este caso, los argumentos serán; el elemento que estamos viendo si forma o no parte del subconjunto y el subconjunto que estamos generando. El caso base es cuando llegamos a revisar si añadir el \( 0 \) que como no está en el conjunto original podemos imprimir el subconjunto.

Código

El código en python utilizando listas puede ser:

def all_subset(n, subset):
  if n == 0:
    print(subset)
  else:
    all_subset(n-1, subset)
    all_subset(n-1, subset + [n])

all_subset(3, [])

El código en C++ utilizando vector puede ser:

#include <iostream>
#include <vector>
using namespace std;

void print_subset(vector<int> subset) {
  for (int i = 0; i < subset.size(); i++) {
    cout << subset[i] << " ";
  }
  cout << endl;
}

void all_subset(int n, vector<int> subset) {
  if (n == 0) {
    print_subset(subset);
  }
  else {
    all_subset(n-1, subset);
    subset.push_back(n);
    all_subset(n-1, subset);
  }
}

int main() {
  all_subset(3, vector<int>());
  return 0;
}

Un problema con esta implementación es que C++ cuando utiliza un vector como argumento, en vez de utilizar la misma dirección, lo copia. Por lo que se está utilizando mucha memoria.

Optimización

En C++ podemos optimizar la memoria utilizando tan solo un vector. Para cada vez que termine una llamada a all_subset se le elimina el último elemento que se le añadió.

#include <iostream>
#include <vector>
using namespace std;

vector<int> subset;

void print_subset() {
  for (int i = 0; i < subset.size(); i++) {
    cout << subset[i] << " ";
  }
  cout << endl;
}

void all_subset(int n) {
  if (n == 0) {
    print_subset();
  }
  else {
    all_subset(n-1);
    subset.push_back(n);
    all_subset(n-1);
    subset.pop_back();
  }
}

int main() {
  all_subset(3);
  return 0;
}

Guía Programación Competitiva